Scientific Machine Learning
Many scientific computing applications such as uncertainty quantification (UQ), inverse problems, and system optimization, are solved by outer loop algorithms that require repeated runs of forward simulations. The computational cost of each inner loop run is typically large, as forward simulations are complex physical models. At the same time, the number of forward runs required for an accurate outer loop solution is also large, either because of the number of outer optimization iterations, or the number of Monte-Carlo samples needed.
To alleviate the large computational costs it is imperative to develop inexpensive surrogate models that when called upon can replace the repeated runs of expensive physics-based models. Construction of accurate surrogates for complex models is challenging. Traditional model order reduction approaches are limited to approximating dynamics in a linear subspace. Nonlinear approximation approaches such as deep learning are needed to fully capture complex behavior , but conventional data-driven models perform poorly when training data is limited.
A promising paradigm for nonlinear surrogate model construction is Scientific machine learning (SciML) that combines traditional machine learning approaches, leveraging existing data, with knowledge of the governing equations. Including first principles into ML models can significantly improve their results. However, current physics-informed surrogates suffer from several shortcomings:
- Even well-trained surrogate models do not automatically guarantee an accurate approximation of model derivatives, which are critical for many outer loop applications.
- Most surrogates do not quantify the uncertainty in their outputs. This is a necessity, as the quality of the surrogate predictions directly impacts the outer loop results.
- Surrogate models need to be retrained during outer-loop iterations to capture the physics as the operating point changes. One needs robust surrogates that remain accurate for a wide range of physical regimes
Projects
Physics-informed neural networks for PDE-constrained optimization and control
- Design of open loop Physics-informed Neural-Network controllers by including the optimality conditions (Pontryagin’s minimum principle equations) in the training loss of neural networks to create single-loop methods that solve forward and backward problems simultaneously for optimal state, control, and adjoint trajectories. For more information read this project’s publication here.
Physics-informed neural networks for inverse problems
- Solving inverse problems using low-resolution observations and Deep Operator Networks. A particular focus is placed on leveraging a limited set of high-resolution direct numerical simulation data in conjuction with sparse observations to infer the parameters of nonlinear choatic dynamical systems and PDEs.
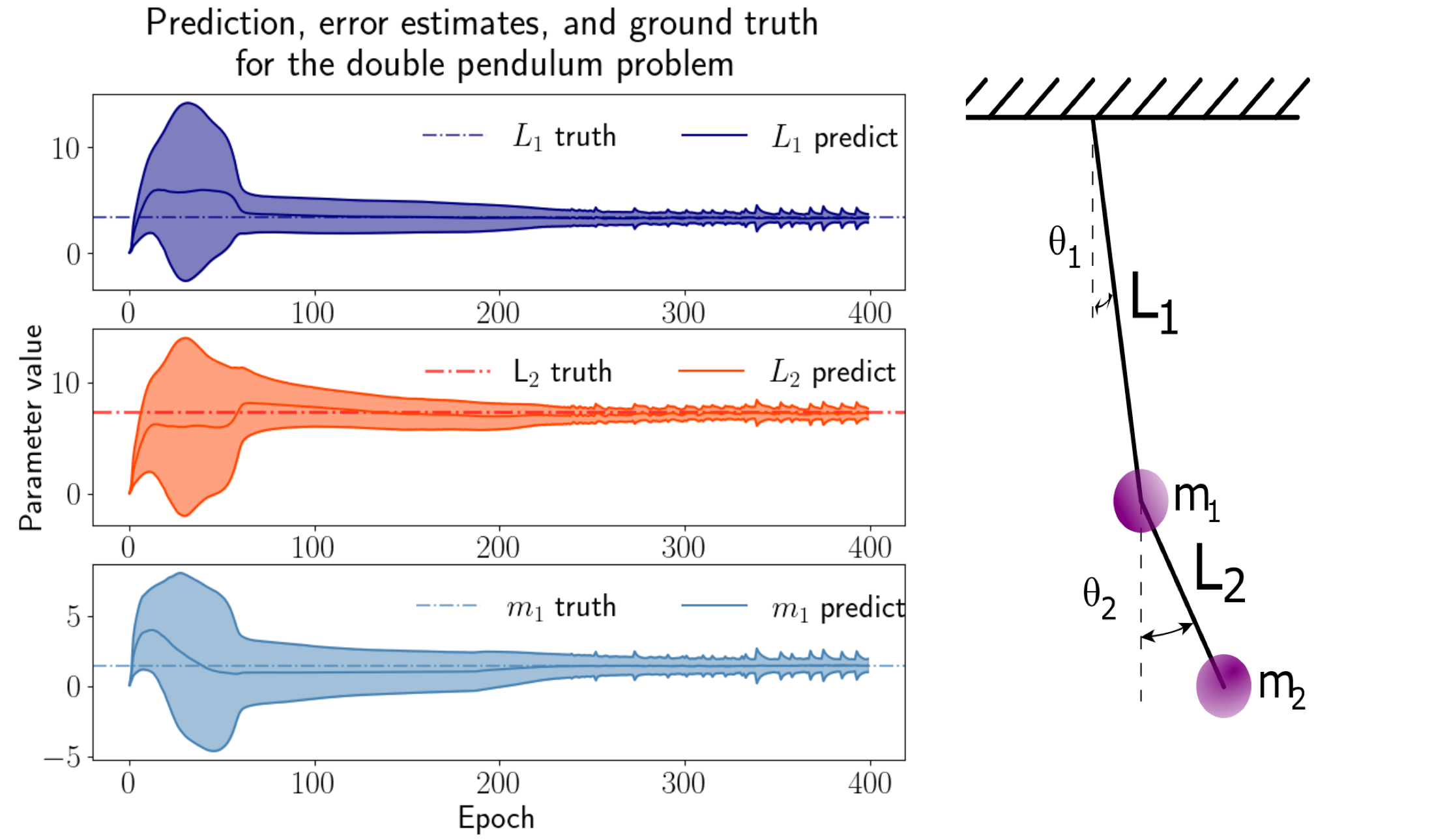
Robustifying Deep Neural networks using high-order derivatives.
Compute the data perturbation directions that have the largest impact on the trained network weights, change in loss, or other quantities of interest using first and second order perturbation analysis (gradients and Hessian-vector products, respectively). We will use this information in adversarial training of the model such as to construct more robust deep learning models.
This approach is extendable to identify additional datapoints that contribute significantly to the generalization capacity of the model, for use in continued training.
